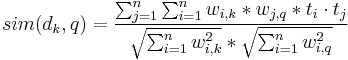Generalized vector space model

The Generalized vector space model is a generalization of the vector space model used in information retrieval. Wong et al.[1] presented an analysis of the problems that the pairwise orthogonality assumption of the Vector space model(VSM) creates. From here they extended the VSM to the generalized vector space model (GVSM).

Definitions

GVSM introduces term to term correlations, which deprecate the pairwise orthogonality assumption. More specifically, they considered a new space, where each term vector ti was expressed as a linear combination of 2n vectors mr where r = 1...2n.

For a document dk and a query q the similarity function now becomes:

sim(d_k,q) = \frac{\sum _{j=1}^n \sum _{i=1}^n w_{i,k}*w_{j,q}*t_i \cdot t_j }{\sqrt{\sum _{i=1}^n w_{i,k}^2}*\sqrt{\sum _{i=1}^n w_{i,q}^2}}

where ti and tj are now vectors of a 2n dimensional space.

Term correlation 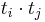t_i \cdot t_j can be implemented in several ways. As an example Wong et al. use as input to their algorithm the term occurrence frequency matrix obtained from automatic indexing and the output is term correlation between any pair of index terms.

Semantic information on GVSM

There are at least two basic directions for embedding term to term relatedness, other than exact keyword matching, into a retrieval model:

  1. compute semantic correlations between terms
  2. compute frequency co-occurrence statistics from large corpora

Recently Tsatsaronis[2] focused on the first approach.

They measure semantic relatedness (SR) using a thesaurus (O) like WordNet. It considers the path length, captured by compactness (SCM), and the path depth, captured by semantic path elaboration (SPE). They estimate the 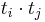t_i \cdot t_j inner product by:

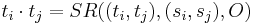
t_i \cdot t_j = SR((t_i, t_j), (s_i, s_j), O)

where si and sj are senses of terms ti and tj respectively, maximizing 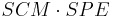SCM \cdot SPE.

References

  1. ^ Wong, S. K. M.; Wojciech Ziarko, Patrick C. N. Wong (1985), Generalized vector spaces model in information retrieval, SIGIR ACM, http://doi.acm.org/10.1145/253495.253506 
  2. ^ Tsatsaronis, George; Vicky Panagiotopoulou (2009), A Generalized Vector Space Model for Text Retrieval Based on Semantic Relatedness, http://www.aclweb.org/anthology/E/E09/E09-3009.pdf